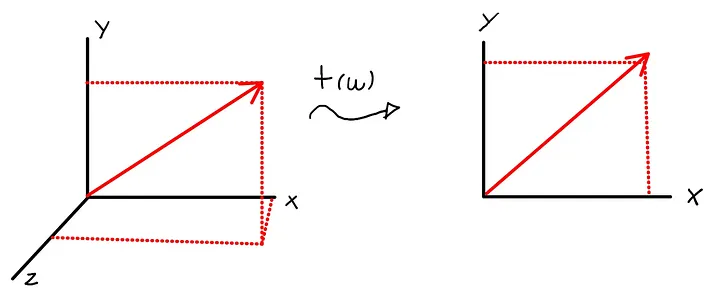
Applications in Computer Science
Linear transformations play a fundamental role in the study of Linear Algebra, Calculus, Differential Equations, Differential Geometry, and various other mathematical disciplines. Moreover, their significance extends to numerous practical applications across different fields.
In computer graphics, linear transformations play an essential role in manipulating pixels on the computer screen. This process is fundamental to bringing images to life, contributing to the creation of high-quality graphics and visual animations.
Revisiting Functions
A function is a relationship between a set of inputs (the domain) and a set of possible outputs (the co-domain). The domain is the set of all possible inputs of a function, and the co-domain is the set of its possible outcomes or results.
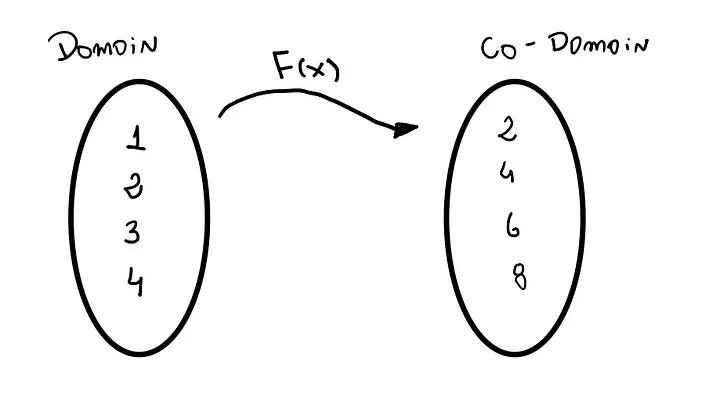Domain and Co-domain of a Function.
Linear Transformation
A linear transformation behaves like a function but the domain and the co-domain are vector spaces while the elements being manipulated are vectors.
Consider a simple linear transformation $$ T: R²->R² $$ Defined by: $$ T(x,y) = (2x,y) $$ This transformation takes two-dimensional vector (x,y) as input and produces a new vector in the co-domain R² by doubling the first component while leaving the second component unchanged.
To illustrate, let’s take a specific vector: $$ u = (2,1) $$ and apply the transformation T to it. The result is shown below:
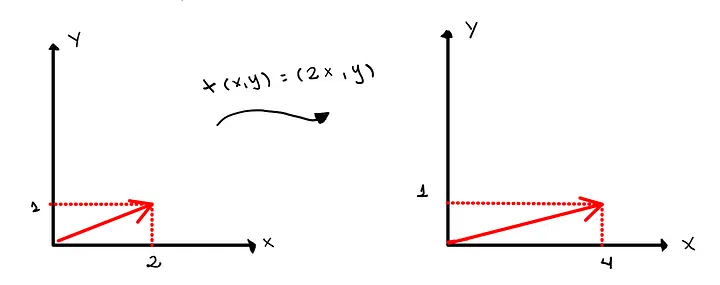
In the geometric sense, this linear transformation represents a scaling along the x-axis by a factor of 2.
A Better Definition
A linear transformation often referred to as a linear map, is a mathematical function T: Rn→Rm that exhibits and satisfies the following fundamental properties:
Additive: $$ T(x + y) = T(x) + T(y), for x,y ∈ Rn. $$
Homogeneity: $$ T(ax) = a T(x) $$ for x ∈ Rn and a ∈ R.
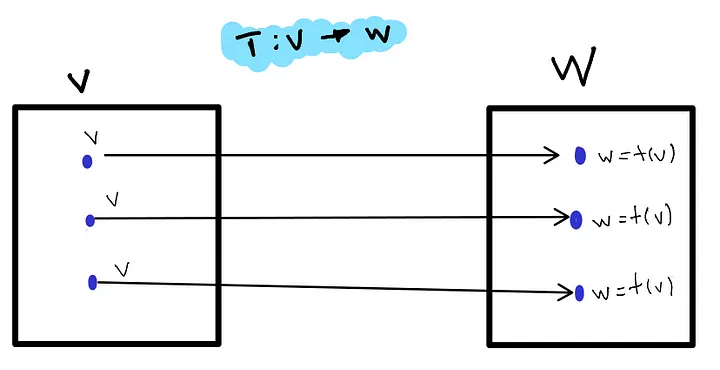V and W are vector spaces. T: V ->W denotes a linear transformation. Each vector v in V maps uniquely to w in W
The Matrix of Transformation
Some linear transformations can be represented geometrically, as exemplified by $$ T(x,y) = (2x,y) $$ These representations find applications in various areas of computer graphics where there is a need to manipulate the content of a scene. Changes in shape, size, and orientation are all intricately linked to geometric transformations.
All geometric transformations can be represented in the form of equations. However, manipulating graphic objects often involves numerous simple arithmetic operations. Matrices are widely used in these manipulations because they are easier to use and understand than algebraic equations. This ease of use explains why programmers and engineers use them extensively.
The matrix serves as a concise and efficient way to represent complex transformations on graphical objects.
Let’s consider a 2D transformation where we want to upscale an object by the factor of two, so we need to have a transformation that looks like: $$ T(x,y) = (2x, 2y) $$ which can be written in matrix form as:
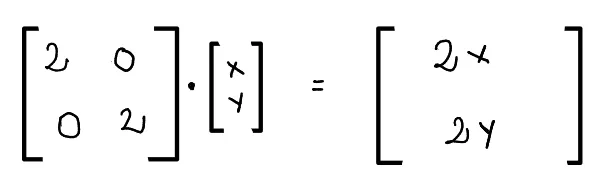The transformation rule encapsulated by the matrix.
The most common geometric transformations are:
Resize
Rotation
Translation
Mirror
Shearing
Resize
This transformation often referred to as expansion, dilation, or contraction, is widely used when we want to make an object appear larger or smaller, in other words, to change its scale. When we zoom in or out on a photograph to enlarge or reduce it, we are applying a scaling transformation.
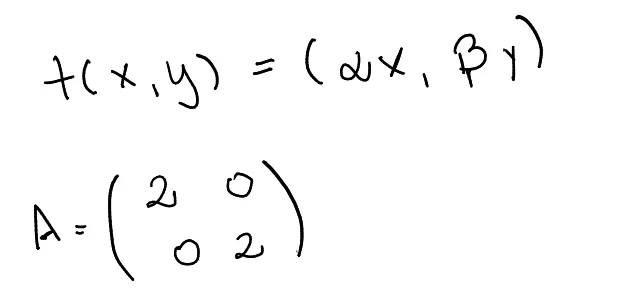
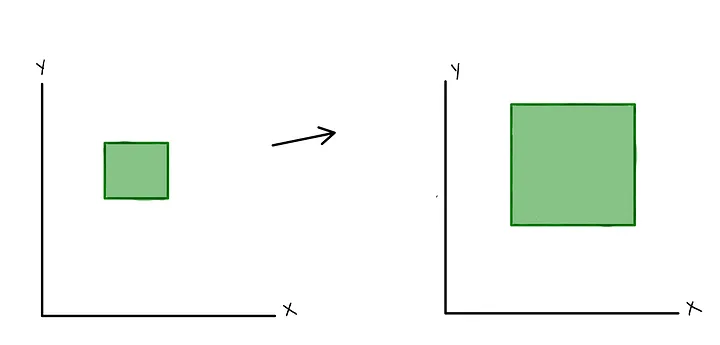Example of a scaling linear transformation.
Rotation
This transformation rotates the object in the plane, either clockwise or counterclockwise, around a base point, which can be one of the object’s vertices or an external point. A real-world scenario would be when you have a photo that’s upside down on its side, and you want to set it straight, that’s when you apply a rotation transformation. In robotics rotation matrices are fundamental for representing and controlling the orientation of robotic components. They enable precise movement planning, coordination, and control.
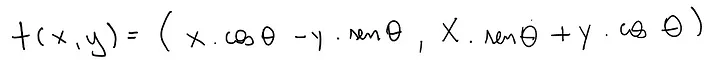Equation of rotation transformation.
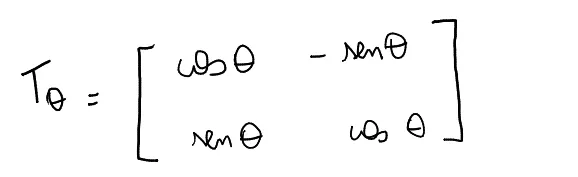Matrix of Transformation.
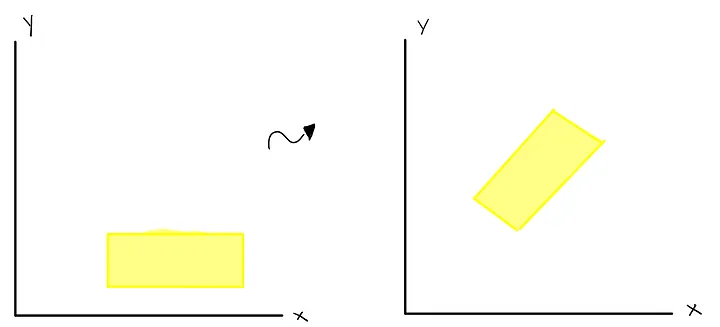Rotation of an object in a plane.
Translation
Translation allows us to move objects within the plane, either horizontally, vertically, or a combination of both. These shifts do not affect the measurements of distances or alter the angles of the objects. When an object undergoes a translation, it maintains its size and shape, changing solely in its position. This concept is exemplified in the figure.
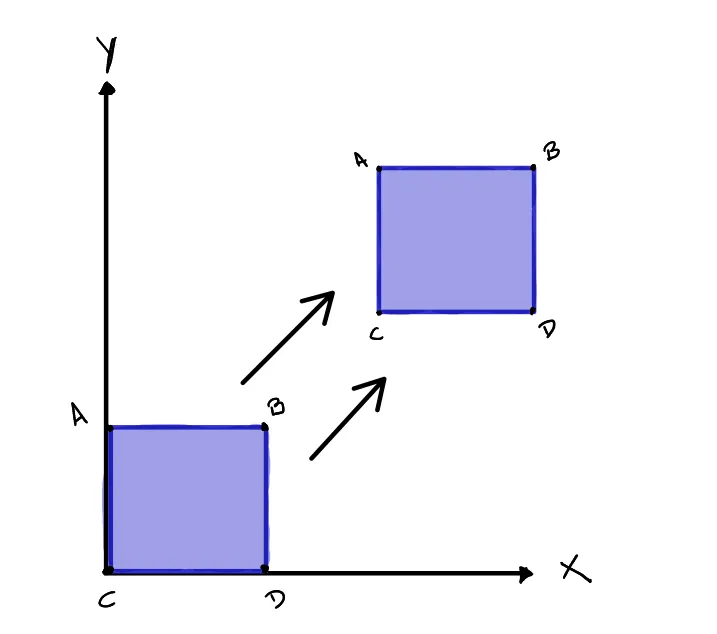Example of translation.
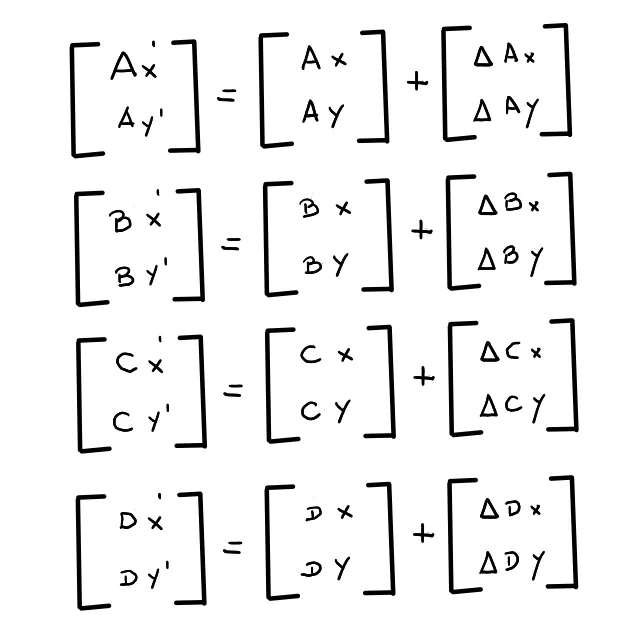Matrix equation representing the new position of the object.
Translation is like moving points in space, but it’s not just multiplying them by a matrix. When we multiply by a matrix, the point at the center (origin) stays the same. However, with translation, even the center point moves. That’s why we can’t represent it as a matrix multiplication.
In the figure below, we can observe an example of a translation application in the movement of dragging and dropping. The computer updates the object by erasing and recreating it with its new coordinates, creating the impression that it is in motion. The same effect occurs with the simple movement of the mouse on the screen.
Drag and Drop.
Mirror
The reflection transformation applied to an object produces a mirrored object concerning one or both axes. This is widely used in graphic design when the goal is to create a reverse copy of the image.
Reflection across the x-axis:
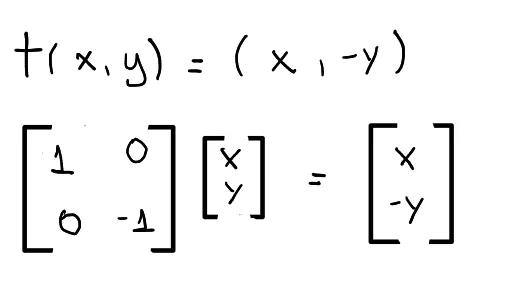Equation and matrix of mirror transformation across x-axis.
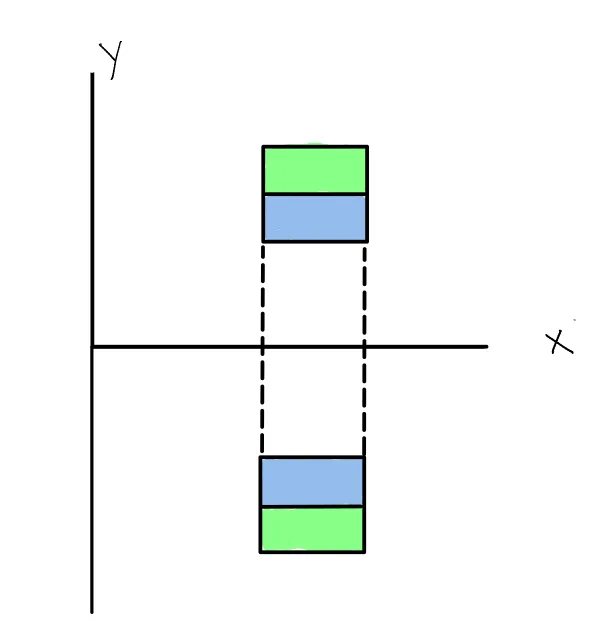Visual Example of reflection in x-axis.
Reflection across the y-axis:
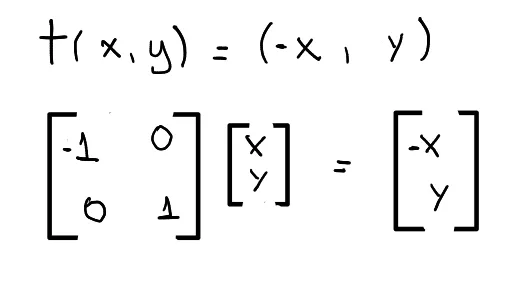Equation and matrix of mirror transformation across y-axis.
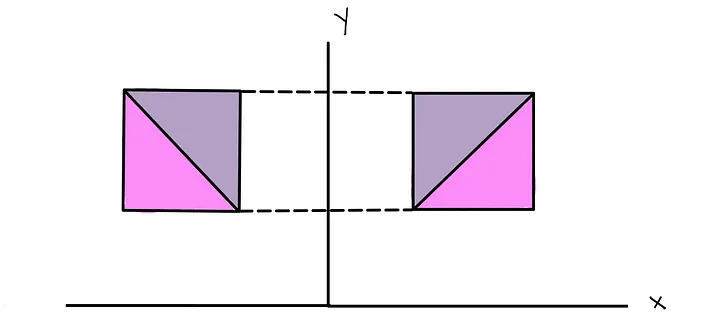Visual example of mirror transformation in y-axis.
Shearing
The shear transformation distorts the object in one or both of its coordinates. It is widely used in image distortion filters in graphic design programs.
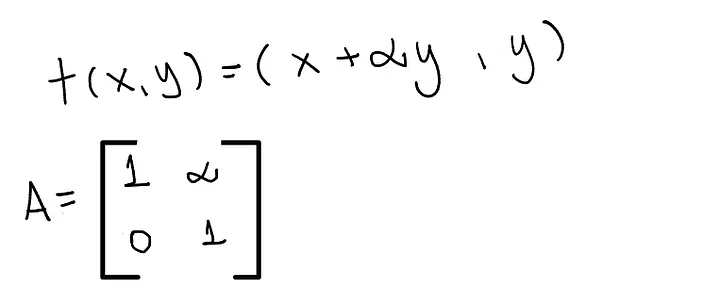Equation and Matrix of horizontally shearing.
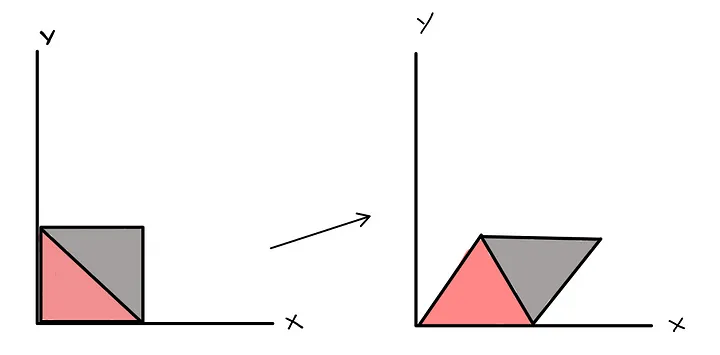Horizontally shearing.
These geometric transformations are fundamental tools in computer graphics and image processing, providing the basis for creating visually appealing and dynamic graphical content.
References
ANTON, H., & RORRES, C. (2004). Elementary Linear Algebra — Applications Version. Wiley.
KOLMAN, B., & Hill, D. (2008). Linear Algebra with Applications. New Jersey: Pearson Education.
VINCE, J. (2006). Mathematics for Computer Graphics 2ª Edition. London: Springer-Verlag