Introdução às Redes Neurais: Perceptron

Essa será uma série de posts, onde pretendo cobrir a principal arquitetura de rede neural: O Perceptron, que fornece a base de outras arquiteturas famosas.

O intuito é implementar cada uma dessas 3 arquiteturas utilizando apenas o Python e o numpy, sem a utilização de frameworks como PyTorch ou TensorFlow.

Esse artigo requer zero conhecimento prévio em Machine Learning ou Deep Learning, mas conhecimento nesses tópicos te ajudaria a compreender melhor alguns conceitos.

Python: o básico sobre orientação à objetos e numpy, já que as implementações serão feitas com essas ferramentas.
Cálculo: os conceitos do cálculo serão utilizados quando o gradiente for calculado durante o processo de treinamento das redes neurais.
Álgebra Linear: Conhecimentos básicos como operações com matrizes, matrizes são a melhor forma de representar os pesos das redes neurais.

Neurônio Artificial

A unidade básica de uma rede neural é o neurônio artificial, como monstrado na capa. O percetron é a forma mais simples de configuração de uma rede neural, idealizado por Rosenblatt em 1958, tinha o próposito de imitar o funcionamento da retina humana.

Funcionamento do Perceptron

A simplicidade da arquitetura do Perceptron também reflete no seu princípio de funcionamento. O perceptron abaixo possui 2 inputs representados por $ x_1 $ e $ x_2 $ e um output representado por $ y $.

Perceptron Simples

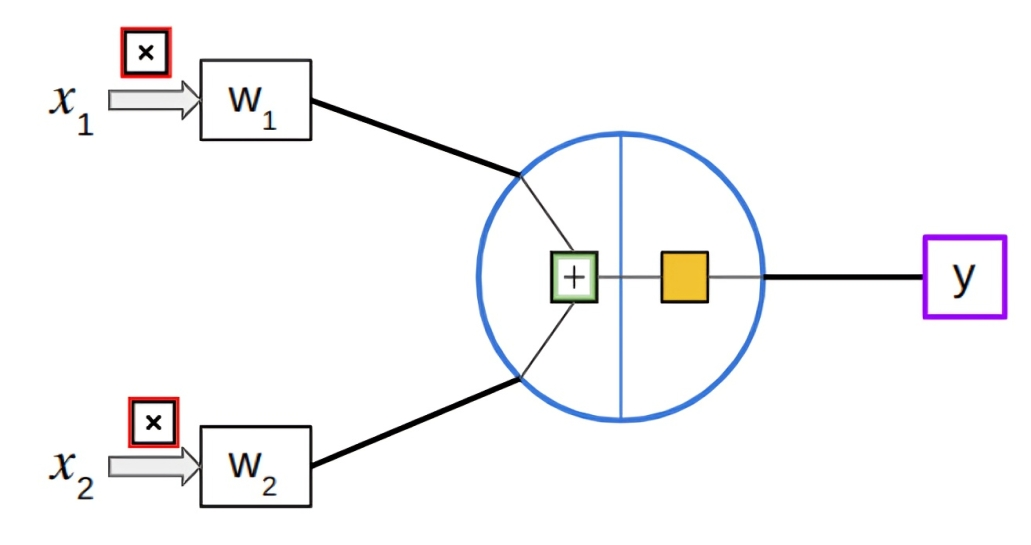
Inicialmente podemos observar que os inputs $x_1$ e $x_2$ estão sendo multiplicados por $w_1$ e $w_2$ respectivamente, e depois são somados (quadrado verde). Então podemos representar essa fase inicial como: $$ (x_1 * w_1) + (x_2 * w_2) $$

Antes de passarem pelo quadrado amarelo (função de ativação) é adicionado um viés (bias) a nossa soma:

$$ (x_1 * w_1) + (x_2 * w_2) + b $$

Porquê o bias é importante ?

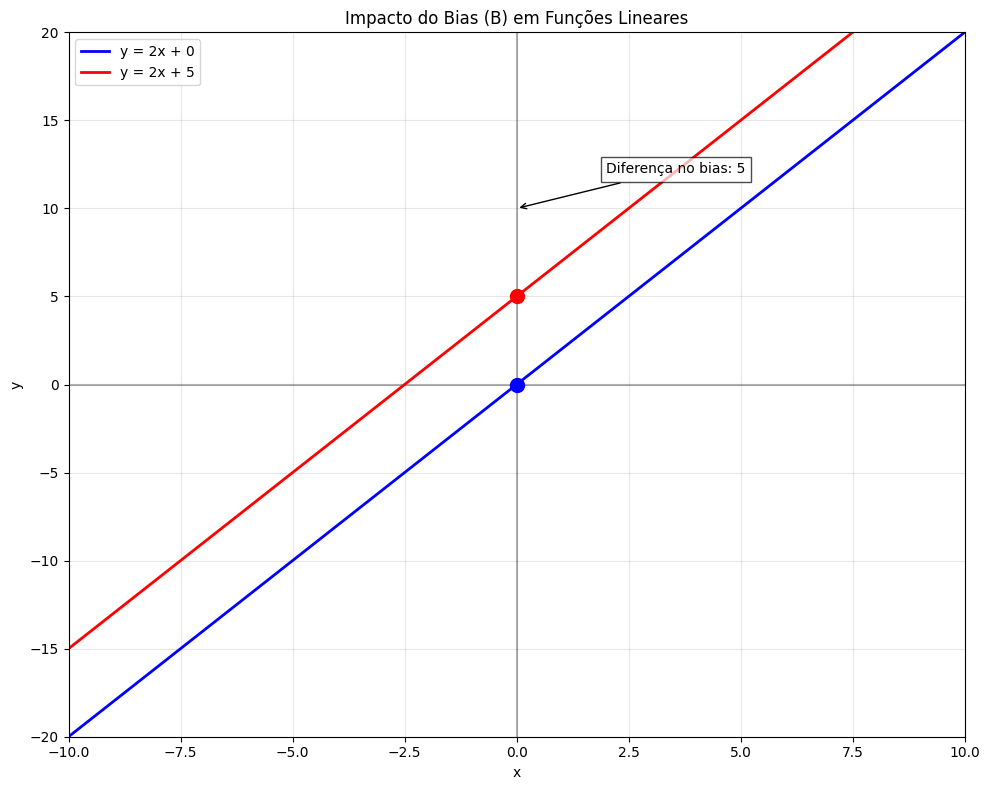
O bias é importante pois ajuda a ajustar a saída $y$ mesmo que todas as entradas sejam zero. ele permite que o modelo aprenda padrões mais complexos ao deslocar a função de ativação para cima ou pra baixo, semelhante ao que acontece na clássica equação da reta

Exemplo de duas retas com bias 0 e 5, note que ele desloca a função para cima ou para baixo. Retas

Função de Ativação

Nota: É mais comum, na arquitetura perceptron utilizar a função degrau, entretanto optei pela sigmoid por simplicidade, já que posteriormente na parte 2, também vou utiliza-lá.

Após ser adicionado ao víes nossa equação ficou: $$ (x_1 * w_1) + (x_2 * w_2) + b $$

Para facilitar, vamos armazenar esses valores em uma outra variável $u$, então:

$$ u = (x_1 * w_1) + (x_2 * w_2) + b $$

Agora vamos aplicar a função de ativação tomando como parâmetro nosso valor $u$:

$$ f(u) $$

Mas qual será nossa função de escolha ? Existem várias funções de ativação que podemos utilizar, entretanto nesse exemplo vamos aplicar a popular função de ativação Sigmoide

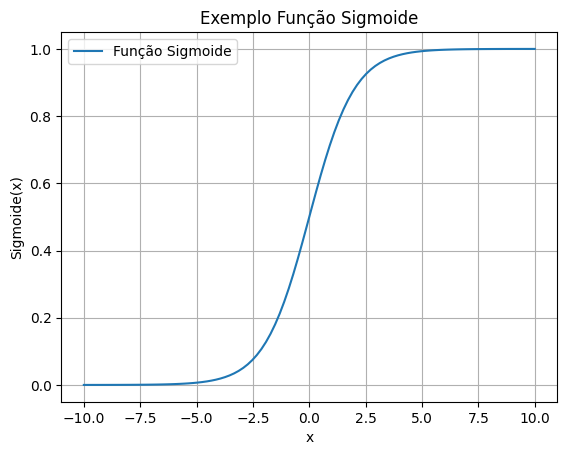
Sigmoide Function

O propósito da função sigmoide é bem definido: para qualquer que seja o input, nosso output estará no intervalo entre 0 e 1.

A sigmoide é definida como:

$$ \sigma(x) = \frac{1}{1 + e^{-x}} $$

Calculando um output de exemplo para o perceptron

Já temos tudo que é necessário para calcular o output de nosso perceptron de exemplo, esse processo de “passar” os valores pela rede é conhecido por feedfoward propagation, no português é conhecido como propagação direta.

Parâmetros do Perceptron:

2 Inputs, $x_1$ e $x_2$
2 Pesos, $w_1$ e $w_2$
Bias, $b$

Valores

Inputs: $x_1 = 0.5$ $x_2 = -0.2$
Pesos: $w_1 = 0.8$ $w_2 = -0.5$
Bias: 1

Cálculo dos Valores

Soma ponderada e bias $$ ( 0.5 * 0.8 ) + ( -0.2 * -0.5 ) + 1 $$

$$ 0.4 + 0.1 + 1 = 1.5 $$

Função de Ativação Sigmoide $$ f(1.5) \approx 0.8175 $$

O neurônio obteve aproximadamente 0.8175, dado os inputs de 0.5 e -0.2. esse processo de passar os inputs através da rede é conhecido como feedforward, como foi dito anteriormente.

Abstraindo o Perceptron através da Orientação à Objetos

Agora que conhecemos o funcionamento do perceptron, conseguimos criar nosso própio módulo python que abstrair o perceptron.

Um bom primeiro exercício, seriamos pensar o que o perceptron precisa ter, ou seja quais atributos e métodos nossa classe precisa ter.

O perceptron deve conter, como visto anterirormente:

Inputs
Pesos
Bias
Função de Ativação

Vou começar, por simplicidade à implementar a função sigmoide:

import numpy as np

def sigmoide(x: float) -> float:
    """ Calcula a função sigmoide, para um dado valor x

    A função sigmoide é definida como: f(x) = 1 / (1 + e^(-x))
    Converte o input entre um intervalo de 0 e 1.

    Argumentos: 
        x: É o valor que será aplicado a função
    Retorno:
        Retorna um valor de ativação entre 0 e 1
    """
    return 1 / (1 + np.exp(-x))

Antes de implementar nossa classe perceptron, precisamos descobrir como representar os pesos e os bias,para isso vamos utilizar uma lista. Como boa prática podemos deixar o usuário decidir se vai utilizar uma lista padrão do python ou uma lista da biblioteca Numpy. Para isso vamos definir um tipo customizado Union.

from typing import Union, List
import numpy.typing as npt

Lista = Union[List[float], np.ndrarray]

Pronto! dessa maneira deixamos o usuário escolher entre uma lista python, ou uma lista numpy utilizando a Union, a union nos diz que nosso tipo Lista pode ser tanto uma list ou um numpy array.

    # perceptron.py
    class Perceptron:
        """ Classe que representa um neurônio artificial (Perceptron)"""

        def __init__(self, pesos: Lista, bias: float) -> None:
            """ Inicializa o perceptron com os pesos e bias

            Argumentos:
                pesos: Lista de pesos do tipo python list, ou numpy array.
                bias: float que representa o bias
            """
            self.pesos = np.array(pesos, dtype=float)
            self.bias = float(bias)

        def feedforward(self, inputs: Lista) -> float:
            """ Processa os inputs através do neurônio 
            artificial usando os pesos o bias e a função de ativação sigmoide
            
            Argumentos: Lista de inputs da rede neural
            Retorno: Valor obtido da função de ativação
            """
            inputs = np.array(inputs,dtype=float)
            if inputs.shape != self.pesos.shape:
                raise ValueError(
                    f"As dimensões do input:{input.shape} devem ser as mesmas dos pesos: {self.pesos.shape}"
                )
            total = np.dot(self.pesos, inputs) + self.bias
            return sigmoid(total)

Nossa classe Perceptron está pronta ! e abstrai toda a estrutura matemática do perceptron (inputs, pesos, bias, função de ativação, e feedforward).

Agora é hora de testar o nosso código:

def main() -> None:
    """Exemplo da nossa classe Perceptron"""

    # Inicializa os pesos e o bias do perceptron
    pesos = np.array([0.8, -0.5]) 
    bias = 1.0                      

    # Cria nosso perceptron
    perceptron = Perceptron(pesos, bias)

    # Testa nossos inputs
    test_input = np.array([0.5, -0.2])  

    # Calcula o output do perceptron
    output = perceptron.feedforward(test_input)
    print(f"Output do Perceptron: {output:.4f}")


if __name__ == "__main__":
    main()

Output do Perceptron: 0.8175

Note que obtivemos o mesmo valor de quando calculamos no “papel”!

Os próximos passo seria utilizar o Pytorch ou TensorFlow para resolver problemas complexos.

Introdução às Redes Neurais: Perceptron#

Neurônio Artificial#

Funcionamento do Perceptron#

Porquê o bias é importante ?#

Função de Ativação#

Calculando um output de exemplo para o perceptron#

Parâmetros do Perceptron:#

Valores#

Cálculo dos Valores#

Abstraindo o Perceptron através da Orientação à Objetos#